Representation of a detection algorithm based on Holt-Winters forecasting
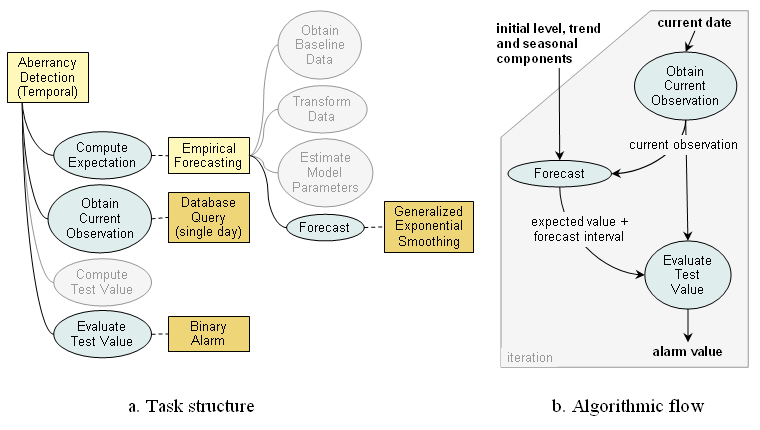
The task structure of the algorithm based on Holt-Winters forecasting is shown in Figure a. Similarly to simpler exponentially weighted moving average techniques, the Holt-Winters filter requires initial values for level, trend and seasonal coefficients. We will assume that these values were obtained beforehand and are not part of the aberrancy detection algorithm, and thus the Obtain Baseline Data, Transform Data and Estimate Model Parameters tasks of the Empirical Forecasting task-decomposition method will be omitted. This is a typical use of the Holt-Winters technique. The Forecast task is performed by the Generalized Exponential Smoothing method that uses an autoregressive approach: it first computes expected value based on the estimates of level, trend and seasonality from the previous step, and then updates these estimates based on the new observation.
Obtain Current Observation retrieves a single data value from the current test period. This observation is not transformed and is used directly as a test statistics, thus the Compute Test Value task is skipped.
The Evaluate Test Value task is accomplished by the Binary Alarm method. Many implementations of the Holt-Winters forecasting generate interval forecasts: they compute a confidence interval in addition to an expected value. The Binary Alarm method can use the upper side of this interval as an alerting threshold, against which it compares the current observation.
The flow diagram for Holt-Winters algorithm is displayed in Figure b. As in the example of the CDC C-family algorithms, all the tasks are repeated at each observation step. There is an important difference, however, in the use of tasks’ initial inputs. The Obtain Current Observation task uses new date at each execution step, which is supplied and updated by the surrounding iteration control structure (shown as shaded area in the figure). The initial values of level, trend and seasonal coefficients, in contrast, are only used once to start up the algorithm. After initialization, the Generalized Exponential Smoothing method performing the Forecast task internally updates these values and stores them for the next step.
← Back to Models